QCCs for patterns

NCTM Standards for patterns

Mathematics is sometimes defined as the science of patterns. What do we mean by a "pattern"? A mathematical pattern involves regularity. This regularity may manifest itself in shape, direction, orientation, size, or number relationships, among other things. The key to being a pattern is that there is some regularity that can be repeated, extended, or built upon.

Recommended Investigations 

Extension: What if you used four consecutive even counting numbers in the above problem? Would your rule change? If so, what would the new rule be? Explain why this new rule works and why it is different from the original rule. If the rule does not change, would your explanation change?

Extension: What if you used four consecutive counting numbers? Would your rule change? If so, what would the new rule be? Explain why this new rule works and why it is different from the original rule(s). If the rule does not change, would your explanation change?

Related External Links:

• The Tower of Hanoi Puzzle - Find a relationship between the least number of turns and number of discs in this famous game. The links available show you sources that give you opportunities to play the game online.
• The Complex Apartment Complex - Determine how many apartments are in a building that has twice as many apartments on each floor.

	T
			1	2	3	4	5	6	7	8	9	10	11	12	13
	1		4	7	12	19	28	39	52	67	84	103	124	147	172
	2		13	16	21	28	37	48	61	76	93	112	133	156	181
S	3		28	31	36	43	52	63	76	91	108	127	148	171	196
	4		49	52	57	64	73	84	97	112	129	148	169	192	217
	5		76	79	84	91	100	111	124	139	156	175	196	219	244
	6		109	112	117	124	133	144	157	172	189	208	229	252	277
	7		148	151	156	163	172	183	196	211	228	247	268	291	316

Related External Links:

• The Twelve Days of Christmas and Pascal's Triangle - This investigation has you examine coloring patterns in Pascal's Triangle that are associated with the number of gifts you receive in the Twelve Days of Christmas song.
• Fractals in Pascal's Triangle - This lesson plan examines coloring patterns in Pascal's triangle that generate Sierpinski's gasket.
• The Tower of Hanoi Puzzle - Find a relationship between the least number of turns and number of discs in this famous game. The links available show you sources that give you opportunities to play the game online.
• The Complex Apartment Complex - Determine how many apartments are in a building that has twice as many apartments on each floor.

Fractions into Whole Numbers
Find three whole numbers, a, b and c, which will make this fraction a whole number:

bc + ac + ab
a + b + c

Can you find a method which will give many such solutions? Explain why this method works.

Related External Links

• Runsums - Find the smallest sum of consecutive groups of numbers.
• Runsums 2 - Find combinations of numbers that produce certain sums.

Could you purchase exactly 17 McNuggets?

How would you purchase exactly 53 McNuggets?

What is the largest number for which it is impossible to purchase exactly that number of McNuggets?

What if the McNuggets were available in boxes of 7, 11, and 17? What is the largest number for which it is impossible to purchase exactly that number of McNuggets?

Related External Links

• Runsums - Find the smallest sum of consecutive groups of numbers.
• Runsums 2 - Find combinations of numbers that produce certain sums.

The sequence named by Fibonacci: 1,1,2,3,5,8,13,21,... can describe the number of family members at each month. Explain how.

Extension: Compare the ratio of consecutive numbers in this sequence. For example 1/1, 1/2, 2/3, 3/5, 5/8, ....What do you notice after a while?

Related External Links:

• Fibonacci Numbers and the Golden Section - This page discuss applications, real world phenomena, puzzles, patterns, and geometry associated with the Fibonacci numbers and golden section.
• Fibonacci Online Assessment - Take a multiple choice quiz that tests your knowledge about Fibonacci, the Fibonacci sequence, and the golden ratio.
• Golden Exploration Worksheet - This worksheet from Mathematics Teaching in the Middle School leads students to discover the golden ratio by making various measurements and calculations.
• The Fibonacci Numbers, Pineapples, Sunflowers and The Golden Mean - Learn how you can find the Fibonacci's sequence on a pineapple.
• Math Course on the Fibonacci Numbers - View the series of lecture notes used for a class exclusively about the Fibonacci numbers.
• A Day at the Arcade - Determine how many ways a coin machine can receive money to exchange for game tokens.

What is the relationship between the seventh terms and sum of the terms of your sequence? What is the relationship between the seventh and tenth term of your sequence? Explain.

Extension: Would your result be different if you started with negative numbers or fractions?

Related External Links:

• Fibonacci Numbers and the Golden Section - This page discuss applications, real world phenomena, puzzles, patterns, and geometry associated with the Fibonacci numbers and golden section.
• Fibonacci Online Assessment - Take a multiple choice quiz that tests your knowledge about Fibonacci, the Fibonacci sequence, and the golden ratio.
• Golden Exploration Worksheet - This worksheet from Mathematics Teaching in the Middle School leads students to discover the golden ratio by making various measurements and calculations.
• The Fibonacci Numbers, Pineapples, Sunflowers and The Golden Mean - Learn how you can find the Fibonacci's sequence on a pineapple.
• Math Course on the Fibonacci Numbers - View the series of lecture notes used for a class exclusively about the Fibonacci numbers.
• A Day at the Arcade - Determine how many ways a coin machine can receive money to exchange for game tokens.

Extension: Generate a shortcut to check the total number of fish caught throughout the tournament by using only the first day's catch, last day's catch, and number of days in the tournament. Explain your reasoning.

Related External Links:

• Sequence of Exercise - Determine how long a pair of people have been running if they continue to run a certain amount farther each day.
• The Name Game - Determine how many names are stated when a teacher learns all of the names in the class.
• Gauss - This is a lesson around the method Gauss used to find the sum of the first 1000 natural numbers.

1/2 + 2/4 + 3/8 + 4/16 + 5/32 + . . .

1/2 + 3/4 + 5/8 + 7/16 + 9/32 + . . .

1/1 + 1/2 + 1/3 + 1/4 + 1/5 + ...

Explain how you found your answers.

Related External Links:

• The Name Game - Determine how many names are stated when a teacher learns all of the names in the class.
• I Know a Secret - This problem investigates how long it takes for a rumor to spread in a school.
• Visualizing an Infinite Series - View the consecutive terms of a geometric series in terms of the areas of segmented trapezoids.

Pascal's Patterns
What is the sum of each row? Find a way to describe the pattern of sums when comparing it to the row number.

Extension: What other patterns do you notice in this triangle of numbers?

Related External Links:

• Antonio's Pizza Palace - This problem investigates how many different possible types of toppings you could have on a pizza.
• The Twelve Days of Christmas and Pascal's Triangle - This investigation has you examine coloring patterns in Pascal's Triangle that are associated with the number of gifts you receive in the Twelve Days of Christmas song.
• Pascal's Triangle - This lesson plan examines how the terms in Pascal's triangle are associated with proabilities in coin tosses.
• Fractals in Pascal's Triangle - This lesson plan examines coloring patterns in Pascal's triangle that generate Sierpinski's gasket.
• Where Can Pascal's Triangle Be Used? - This set of links connects Pascal's triangle to algebra, biology, fractals, games, geometry, number theory, probability, and puzzles.

Related External Links:

• Pancake Man - Determine how many pancakes someone eats if they double their intake every ten minutes.
• Visualizing an Infinite Series - View the consecutive terms of a geometric series in terms of the areas of segmented trapezoids.

Squares on a Checkerboard
How may squares, of any size, are on a 3 x 3 checkerboard? 4 x 4? 8 x 8? n x n? Explain how you arrived at your answers.

Completing the Sequence
Find the next numbers in each of these sequences:

-4

-1

2

5

8

11

14

17

20

-1

0

3

8

15

24

35

48

63

-128

-54

-16

-2

0

2

16

54

128

Sum of Consecutive Integers
How many integers from 10 to 40 can be written as the sum of 2 consecutive integers?
How many integers from 10 to 40 can be written as the sum of 3 consecutive integers?
How many integers from 10 to 40 can be written as the sum of 4 consecutive integers?

Can you find a pattern? Explain.

The number used to describe each "triangle" is called a triangular number. Given a number, can you arrange that many dots into a triangle? If you can, you have identified a triangular number. The sequence of triangular numbers starts with 1, 3, 6, and so on.

Draw a picture of the next triangle in the sequence and state the next triangular number.

Without drawing any more triangles, determine the next five triangular numbers and explain how you found your results.

Extension: Investigate the pattern with square numbers.

Analyzing and Applying Sequences

							1		1
						2		2		2
					3		4		4		3
				4		7		8		7		4
			5		11		15		15		11		5
		6		16		26		30		26		16		6
	7		22		42		56		56		42		22		7
8																8

Triangles inside Triangles
This triangle starts with the outside diagonal rows 1, 2, 3, 4, 5, 6, 7, 8, . . .

The inside numbers are each the sum of the two numbers in the previous row, above right, and above left. For example, 42 = 16 + 26.

Extend the table and determine a relationship between the numbers in the triangle which are exactly divisible by one specific prime greater than 5 . How do the results change if you try another prime greater than 5?

Infinite Series and Partial Sums

Sum of Natural Numbers
Given that 1 = 1, 1 + 2 = 3, 1 + 2 + 3 = 6, and 1 + 2 + 3 + 4 = 10, what is the sum of the numbers from 1 to 100? Explain how you found your answer.

Extension: What does 1 + 2 + 3 + 4 + 5 + 6 + . . . + n equal? Give your answer in terms of n. Explain your solution.

Repeating Patterns
In the following decimal, how many 2's are there in all before the hundredth 3?

0.23223222322223. . .

Geometric

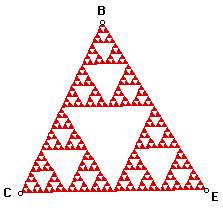
Fractal Iterations
The diagrams below represent the stages involved in constructing a fractal, an infinite pattern where the initial stage is visible in smaller pieces of the image. Each step in the process is called an iteration.

Initial stage
1st iteration
2nd iteration

Draw the 3rd iteration and describe how you made it.

Extension:

Describe how you would generate Sierpinski's triangle shown below.

Tessellating a Plane
The blue parallelogram ABCD shown below has been tessellated so that it tiles a surface without any gaps or overlaps. Name as many other quadrilaterals that can also tessellate a flat surface. Explain your solution.

View a Geometer's SketchPad template or a java applet of this construction to convince yourself.

Extension:

Name as many other individual polygons that can tessellate a flat surface. Justify your answer(s).

Extension:

What combination(s) of polygons can tessellate a flat surface? Explain why those combination(s) work while others do not.

Puzzles

The Next Row
Complete the ???? row in this problem. Explain how you found the solution.

1
11
21
1211
111221
312211
13112221
1113213211
??????????????

The 26th Degree
What is (x-a)(x-b)(x-c)...(x-y)(x-z)? Explain how you found the answer.

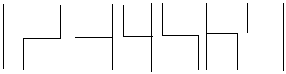
Explain how you determined the result.

Extension: Suppose you can choose the number of sticks at the start of the game. If your opponent goes first, then how many sticks do you want at the start if you want to win every time?

Extension: How would the strategy change if you could pick only 1,2, or 3 sticks during your turn?

interMath Patterns Lesson Resources

Choose one of the categories below or scroll down to view resources related to number patters

Applications and Connections
Lessons, Activities, and Units
Literature
Problem Solving
Puzzles

Applications and Connections
Fibonacci numbers and nature Fabulous Fibonacci phenomena Fibonacci tree and the golden ratio Practical uses for Pascal's triangle Cryptography The Florida Quilt Connection	Fractals in nature The dance of chance Quasicrystals World of Escher B-Eye Morse Code and the Phonetic Alphabets Patterns and Symmetry in Oriental Carpets
Lessons, Activities, and Units
Applications The art of oriental carpets Mirror symmetry Fractals Fractals lesson by Cynthia Lanius Create your own fractal The fractory Fractals- Pascal's Triangle Fibonacci's Sequence Fibonacci in nature Fibonacci online assessment Lecture Notes Golden Ratio The Fibonacci Numbers, Pineapples, Sunflowers and The Golden Mean Series and Partial Sums Sum of numbers from 1 to 100 Gauss	Tessellations Tessellation tutorials Totally Tessellated Tantalizing Tessellations Pascal's Triangle: Word problems, color configurations, and patterns The twelve days of Christmas Fractals Probability Counting General resource and links Discovery, coloring, problem solving Number patterns Visual patterns
Literature

Book titles related to Fibonacci numbers

Chaitin, Gregory J. 1988. Randomness in arithmetic. Scientific American (July):80-85.

Exploring Patterns

Fibonacci Quarterly

Gardner, Martin. 1989. Pascal's triangle. In Mathematical Carnival. Washington, D.C.: Mathematical Association of America.

Garland , T. H. Fibonacci Fun: Fascinating Activities with Intriguing Numbers. Dale Seymour Publications, 1990.

Johnson, A. Now & Then: Fiber Meets Fibonacci. Mathematics Teaching in the Middle School. Reston, Va: NCTM, Jan 1999 Vol 4, No. 4.

Lawler, Robert. Sacred Geometry: Philosophy and Practice. London: Thames & Hudson, 1982.

Little, C. Teacher to Teacher: Geometry Projects Linking Mathematics, Literacy, Art, and Technology. Mathematics Teaching in the Middle School. Reston, Va: NCTM, Feb 1999 Vol 4, No. 5.

NCTM. "Tri-Square" Numbers. Mathematics Teaching in the Middle School. Reston, Va: NCTM, Apr-May 1995, pp. 408-9

NCTM. Exploring Patterns in Nonroutine Problems. Mathematics Teaching in the Middle School. Reston, Va: NCTM, 1999 Vol 4, No. 5. Feb 1997, pp. 262­69

Pattern-Based Math and Science Curriculum

Pickover, Clifford A. 1990. On the aesthetics of Sierpinski gaskets formed from large Pascal's triangles. Leonardo 23(No. 4):411-417.

Runion, Garth. The Golden Section. Palo Alto, Calif.: Dale Seymour Publications, 1990.

Schroeder, Manfred. 1991. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W.H. Freeman.

Sved, Marta. 1988. Divisibility - with visibility. Mathematical Intelligence 10(No. 2):56-64.

Problem Solving
Fibonacci's Sequence Steps in the sun A day at the arcade Simple arithmetic Making money Other Sequences Sequence of exercise The tower of Hanoi puzzle Run sums 2 What digit is it? Geometric Patterns Bricks activity tessellations	Series and Partial Sums The name game The complex apartment complex I know a secret Valentine treats Pancake man Run sums Pascal's Triangle Mrs Pascalini's garden Antonio's pizza palace How many Shamrocks do you see?
Puzzles
It's a secret Nim skulls Tower of Hanoi The Moscow Puzzles - A Pattern The little math puzzle contest Fibonacci Puzzles

Revised September 27, 1999

interMath Patterns History Resources

Choose one of the categories below or scroll down to view historical resources related to patterns

Historical References
Literature
Mathematicians

Historical References
Codebreaking and Secret Weapons in World War II
Tower of Hanoi problem
Development of mathematics in ancient China
Fractal History
Tessellations and mathematics: A logical connection
Totally Tessellated: History

Literature

Boyer, Carl B. 1968. A History of Mathematics. New York: Wiley.

Hofstadter, D. R. Godel, Escher, Bach : An Eternal Golden Braid. Basic Books: 1999.

Johnson, Art. Classic Math: Historical Topics for the Mathematics Classroom. Palo Alto, Calif.: Dale Seymour
Publications, 1992.

National Council of Teachers of Mathematics (NCTM). Historical Topics for the Mathematics Classroom. Reston, Va.:
NCTM, 1969, 1989.

Zaslavsky, C. Africa counts: number and pattern in African culture. Prindle, Weber & Schmidt, Boston, 1973.

Mathematicians
Fibonacci
Gauss
Pascal

click this image to go to opening page